Normalization

Unicode normalization algorithm.

Enumerations 🔗

enum uninormform: Unicode normalization forms.

enum uninormchk: Quick check constants.

Functions 🔗

unistat uni_norm( uninormform form, const void *src, unisize src_len, uniattr src_attr, void *dst, unisize *dst_len, uniattr dst_attr): Normalize text.

unistat uni_normcmp( const void *s1, unisize s1_len, uniattr s1_attr, const void *s2, unisize s2_len, uniattr s2_attr, bool *result): Canonical equivalence.

unistat uni_normchk( uninormform form, const void *text, unisize text_len, uniattr text_attr, bool *result): Normalization check.

unistat uni_normqchk( uninormform form, const void *text, unisize text_len, uniattr text_attr, uninormchk *result): Normalization quick check.

Discussion 🔗

Unicode normalization transforms a string for the purposes of testing equivalence against another string. There are three primary equivalence tests that can be performed:

Binary equivalence: The code points of two strings are compared.
Canonical equivalence: The graphemes of two strings are compared.
Compatibility equivalence: The abstract graphemes of two strings are compared.

Binary Comparison 🔗

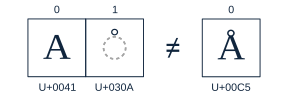
Binary comparison refers to comparing the code points of two strings. In C you can do this with memcmp or strcmp. The drawback of a binary comparison is that two strings that display the same might not be considered equivalent. For example, the strings U+0041 U+030A and U+00C5 represent the same grapheme, but would be considered inequivalent since their code points differ.

Canonical Decomposition 🔗

Canonical decomposition transforms the code points of a string in a predictable way that preserves graphemes. After this transformation is performed on two strings their code points can be compared and, if identical, indicates their graphemes are equivalent.

Compatibility Decomposition 🔗

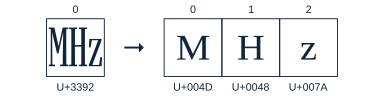
Compatibility decomposition transforms the code points of a string in a predictable way that preserves the abstract meaning of the graphemes. For example, the string U+3392 and U+004D U+0048 U+007A have distinct visual appearances, but identical in meaning. If these strings were compared canonically, they would be considered inequivalent, but when compared for compatibility they are considered equivalent.

Compatibility decomposition is unsupported by Unicorn because it has limited usefulness. It’s intended for fuzzy equivalence tests which are useful in search engines and database queries where the meaning of the string is more important than its visual appearance.

Normalization Forms 🔗

Unicode Normalization Forms are formally defined normalizations of Unicode strings which make it possible to determine whether any two Unicode strings are equivalent to each other. Depending on the particular Unicode Normalization Form, that equivalence can either be a canonical or a compatibility equivalence. Unicorn does not support normalization forms for testing compatibility equivalence, therefore only normalization forms for canonical equivalence testing are available.

To test two strings for canonical equivalence they must be normalized into a normalization form. Unicorn supports two normalization forms for testing canonical equivalence: Normalization Form D (NFD) and Normalization Form C (NFC). The former performs canonical decomposition and the latter canonical composition.

Canonical Composition 🔗

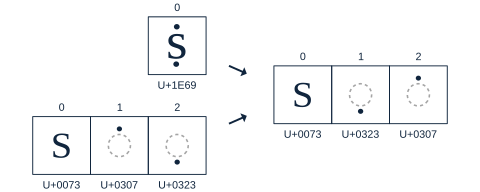
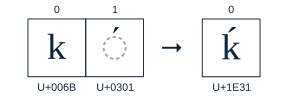
Canonical composition maps multiple code points to a precomposed code point. For example, the string U+006B U+0301 would canonically compose to the code point U+1E31. This is useful for reducing memory consumption and for legacy applications that cannot handle multi-code point graphemes gracefully.

Most real world text is stored in Normalization Form C (NFC). This is because it is more compatible with strings converted from legacy encodings. For example, text exclusively containing ASCII characters is left unaffected by all of the Normalization Forms which is effectively the same as saying that all Latin-1 text is already normalized to NFC.

Additional Observations 🔗

The normal forms are not closed under string concatenation. That is, even if two strings X and Y are normalized, their string concatenation X+Y is not guaranteed to be normalized. By contrast, all Normalization Forms are closed under substringing. For example, the extracted substring of a normalized string X is always normalized.

All normalization transformations are idempotent. Once a string has been normalized it will never change if renormalized to the same normalization form. In other words:

toNFC(toNFC(x)) = toNFC(x)
toNFD(toNFD(x)) = toNFD(x)

More more information on Unicode normalization and normalization forms, see Unicode Technical Report #15.

Manual